algorithm - Find the paths between two given nodes?

Question

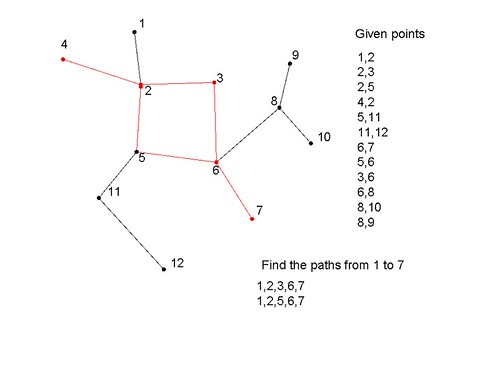
Say I have nodes connected in the below fashion, how do I arrive at the number of paths that exist between given points, and path details?

1,2 //node 1 and 2 are connected
2,3
2,5
4,2
5,11
11,12
6,7
5,6
3,6
6,8
8,10
8,9

Find the paths from 1 to 7:

Answer: 2 paths found and they are

1,2,3,6,7
1,2,5,6,7

implementation found here is nice I am going to use the same

Here is the snippet from the above link in python

# a sample graph
graph = {'A': ['B', 'C','E'],
             'B': ['A','C', 'D'],
             'C': ['D'],
             'D': ['C'],
             'E': ['F','D'],
             'F': ['C']}

class MyQUEUE: # just an implementation of a queue

    def __init__(self):
        self.holder = []

    def enqueue(self,val):
        self.holder.append(val)

    def dequeue(self):
        val = None
        try:
            val = self.holder[0]
            if len(self.holder) == 1:
                self.holder = []
            else:
                self.holder = self.holder[1:]   
        except:
            pass

        return val  

    def IsEmpty(self):
        result = False
        if len(self.holder) == 0:
            result = True
        return result


path_queue = MyQUEUE() # now we make a queue


def BFS(graph,start,end,q):

    temp_path = [start]

    q.enqueue(temp_path)

    while q.IsEmpty() == False:
        tmp_path = q.dequeue()
        last_node = tmp_path[len(tmp_path)-1]
        print tmp_path
        if last_node == end:
            print "VALID_PATH : ",tmp_path
        for link_node in graph[last_node]:
            if link_node not in tmp_path:
                #new_path = []
                new_path = tmp_path + [link_node]
                q.enqueue(new_path)

BFS(graph,"A","D",path_queue)

-------------results-------------------
['A']
['A', 'B']
['A', 'C']
['A', 'E']
['A', 'B', 'C']
['A', 'B', 'D']
VALID_PATH :  ['A', 'B', 'D']
['A', 'C', 'D']
VALID_PATH :  ['A', 'C', 'D']
['A', 'E', 'F']
['A', 'E', 'D']
VALID_PATH :  ['A', 'E', 'D']
['A', 'B', 'C', 'D']
VALID_PATH :  ['A', 'B', 'C', 'D']
['A', 'E', 'F', 'C']
['A', 'E', 'F', 'C', 'D']
VALID_PATH :  ['A', 'E', 'F', 'C', 'D']

Answer 1

Breadth-first search traverses a graph and in fact finds all paths from a starting node. Usually, BFS doesn't keep all paths, however. Instead, it updates a prededecessor function π to save the shortest path. You can easily modify the algorithm so that π(n) doesn't only store one predecessor but a list of possible predecessors.

Then all possible paths are encoded in this function, and by traversing π recursively you get all possible path combinations.

One good pseudocode which uses this notation can be found in Introduction to Algorithms by Cormen et al. and has subsequently been used in many University scripts on the subject. A Google search for “BFS pseudocode predecessor π” uproots this hit on Stack Exchange.