The Wikipedia article also confused me when I read it some time ago. Here is my attempt to explain it differently:
The Situation
Let's simplify the situation. We have:
- Our projected point D(x,y,z) - what you call relativePositionX|Y|Z
- An image plane of size w * h
- A half-angle of view α
... and we want:
- The coordinates of B in the image plane (let's call them X and Y)
A schema for the X-screen-coordinates:
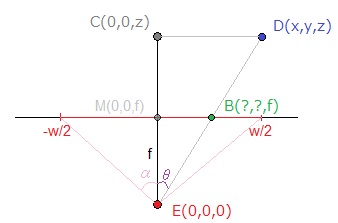
E is the position of our "eye" in this configuration, which I chose as origin to simplify.
The focal length f can be estimated knowing that:
A bit of Geometry
You can see on the picture that the triangles ECD and EBM are similar, so using the Side-Splitter Theorem, we get:
MB / CD = EM / EC <=> X / x = f / z (2)
With both (1) and (2), we now have:
X = (x / z) * ( (w / 2) / tan(α) )
If we go back to the notation used in the Wikipedia article, our equation is equivalent to:
You can notice we are missing the multiplication by s_x / r_x. This is because in our case, the "display size" and the "recording surface" are the same, so s_x / r_x = 1.
Note: Same reasoning for Y.
Practical Use
Some remarks:
- Usually, α = 45deg is used, which means
tan(α) = 1. That's why this term doesn't appear in many implementations.
If you want to preserve the ratio of the elements you display, keep f constant for both X and Y, ie instead of calculating:
X = (x / z) * ( (w / 2) / tan(α) ) and Y = (y / z) * ( (h / 2) / tan(α) )
... do:
X = (x / z) * ( (min(w,h) / 2) / tan(α) ) and Y = (y / z) * ( (min(w,h) / 2) / tan(α) )
Note: when I said that "the "display size" and the "recording
surface" are the same", that wasn't quite true, and the min
operation is here to compensate this approximation, adapting the
square surface r to the potentially-rectangular surface s.
Note 2: Instead of using min(w,h) / 2, Appunta uses screenRatio=
(getWidth()+getHeight())/2 as you noticed. Both solutions preserve the elements
ratio. The focal, and thus the angle of view, will simply be a bit different,
depending on the screen's own ratio. You can actually use any function you want to
define f.
As you may have noticed on the picture above, the screen coordinates are here defined between [-w/2 ; w/2] for X and [-h/2 ; h/2] for Y, but you probably want [0 ; w] and [0 ; h] instead. X += w/2 and Y += h/2 - Problem solved.
Conclusion
I hope this will answer your questions. I'll stay near if it needs editions.
Bye!
< Self-promotion Alert > I actually made some time ago an article
about 3D projection and rendering. The implementation is in
Javascript, but it should be quite easy to translate.
与恶龙缠斗过久,自身亦成为恶龙;凝视深渊过久,深渊将回以凝视…
